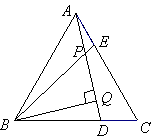
如图，在△ABC中，AB=AC=CB，AE=CD，AD、BE相交于P，BQ⊥AD于Q．求证：BP=2PQ．

答案

∵AB=AC=CB，
∴∠BAE=∠ACD=60°，AE=CD， AB=AC，
∴△BAE≌△ACD，
∴∠ABE=∠CAD
∵∠BPQ=∠ABE+∠BAP ，
∴∠BPQ=∠CAD+∠BAP=60°
∵BQ⊥AD，
∴∠PBQ=30°，
∴BP=2PQ

知识点：含30度角的直角三角形  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>