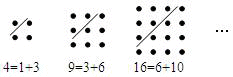古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是(    )

由3-1=2，6-3=3,10-6=4，得下一个数与10的差应该是5，所以这个数是15，
以此类推得，三角形数为：1、3、6、10、15、21、28、36….
“正方形数”依次为正整数的平方：1、4、9、16、25、36、49…..
选项A中的13不是整数的平方， B中9不是三角形数，D中18,31都不是三角形数，不符合题中的规律，故排除。应选C。

没有找到三角形数和正方形数的规律