在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为D，
连接BE．已知AE=13，AD：DE=5:12，则BE+CE=(    )

1．解题要点：
与“直线”相交，提示分类讨论：
①点E在线段AC上时，如图所示，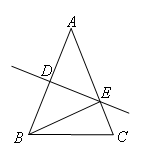

在Rt△ADE中，AD：DE=5:12，AE=13，
∴AD=5，DE=12，
∴AD=DB=5，
∴AB=AC=10．
如图，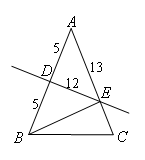

∵AE=13>AC，
∴这种情况不成立；
②点E在射线AC上时，如图所示，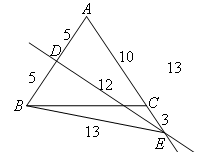

∴CE+BE=16．
③E在射线CA上时，如图所示，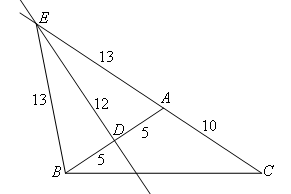

∴CE+BE=36．
∴CE+BE的值可能为16或36．
故选D．
2．解题思路：
见上述解题要点．

略