一纸片的形状为Rt△AOB,其中∠AOB=90°,OA=2,OB=4.将该纸片放置在平面直角坐标系中,如图所示,折叠该纸片,使得折叠后点B与三角形另一顶点重合,折痕与边OB交于点C,与边AB交于点D,则点C的坐标为( )
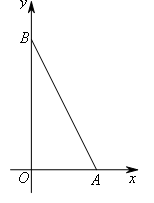
- A.
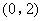
- B.
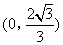
- C.

- D.
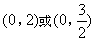
答案
正确答案:D
知识点:分类讨论 翻折变换(折叠问题)
由题意可得,A(2,0),B(0,4).
经过翻折点B可能落在点O处也可能落在点A处,需要分类讨论.
①点B和点O重合,依题意画出对应的图形,如图1,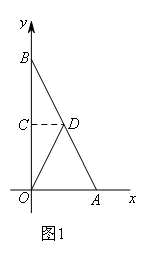
点C为OB的中点,
∴C(0,2).
②点B和点A重合,如图2,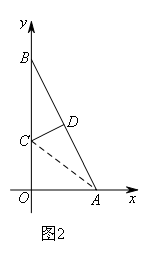
由题意可得,CD⊥AB,且点D是AB的中点.
在Rt△AOB中,OA=2,OB=4,
则![]() ,
,
∴![]() .
.
∵∠BDC=∠BOA=90°,
∴△BCD∽△BAO,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上,点C的坐标为![]() .
.
故选D.
略








