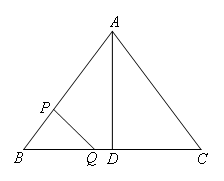
如图,在△ABC中,AB=AC=10,BC=12,D是BC的中点.点P从B出发,以每秒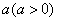 个单位的速度沿BA匀速向点A运动,点Q同时以每秒1个单位的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设它们运动的时间为t秒.
个单位的速度沿BA匀速向点A运动,点Q同时以每秒1个单位的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动.设它们运动的时间为t秒.
(1)若a=2,△BPQ∽△BDA,则t的值为( )
- A.
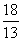
- B.

- C.
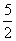
- D.

答案
正确答案:A
1.解题要点
①研究基本图形,将相关数据标注在图形上.
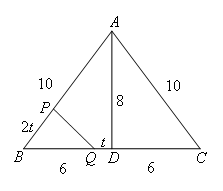
②分析运动状态,分段定范围.
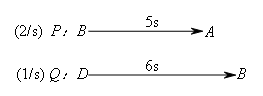
∴![]() .
.
③分析几何特征、表达、设计方案求解.
考虑到条件中△BPQ∽△BDA,用相似符号连接,因此从动点的运动开始表达,根据对应线段成比例建立等式求解.
若△BPQ∽△BDA,则![]() .结合基本图形利用QD=t,BP=2t表达线段长,
.结合基本图形利用QD=t,BP=2t表达线段长,
可得BQ=6-t,进而![]() ,可得
,可得![]() .
.
④结果检验、总结.
作图验证,根据图形对结果进行判断;分析数据,对结果进行验证取舍.
2.解题过程
由题意,BP=2t,QD=t,![]() .
.
∵在△ABC中,AB=AC=10,BC=12,D是BC的中点,
∴BD=DC=6,
∴BQ=6-t.
若△BPQ∽△BDA,则![]() ,
,
∴![]() ,解得
,解得![]() .
.
故选A.
略








