如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3.点P从点B出发,沿BA方向以每秒1个单位长度的速度向点A匀速运动;点Q从点A同时出发,沿AC方向以每秒2个单位长度的速度向点C匀速运动.连接PQ,设运动的时间为t(s)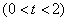 ,解答下列问题:
,解答下列问题:
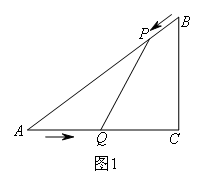
(1)当PQ∥BC时,t的值为( )
- A.
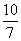
- B.
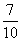
- C.
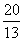
- D.
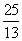
答案
正确答案:A
1.解题要点
①研究基本图形,将信息标注在图形上.
在Rt△ABC中,BC=3,AC=4,AB=5.
②分析运动状态,分段,定范围.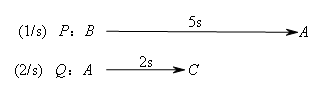
![]() .
.
③分析几何特征、表达、设计方案求解.
由题意得,AQ=2t,BP=t.
∵AB=5,AC=4,
∴AP=5-t,CQ=4-2t,
当PQ∥BC时,利用相似三角形列等式求解.
2.解题过程
在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
由题意,BP=t,AQ=2t,
∴AP=5-t,CQ=4-2t.
当PQ//BC时,如图所示,
△APQ∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
略








