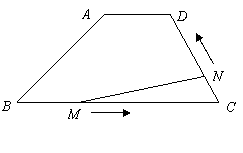
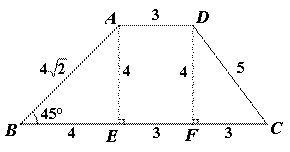
如图,在梯形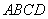 中,
中, 动点
动点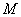 从
从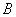 点出发沿线段
点出发沿线段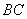 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点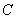 运动;动点
运动;动点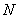 同时从
同时从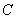 点出发沿线段
点出发沿线段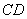 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点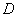 运动.设运动的时间为
运动.设运动的时间为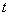 秒.
秒.
(1)求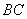 的长.
的长.
(2)当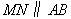 时,求
时,求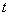 的值.
的值.
(3)试探究: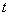 为何值时,
为何值时,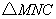 为等腰三角形.
为等腰三角形.
答案
(1)BC=10cm(2)t=s(3)当t=
![]() s,
s,![]() s,
s,![]() s时,△MNC为等腰三角形
s时,△MNC为等腰三角形
知识点:运动变化型问题
第一步:研究基本图形.
第二步:分析运动过程,研究动点的起点、终点,确定时间范围.
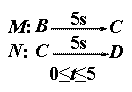
第三步:表达,根据几何特征建等式.
(1)研究基本图形时候BC已经求出,BC=10cm.
(2)当MN∥AB时,我们先画出相应图形:
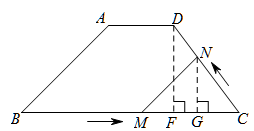
BM=2t,CM=10-2t,CN=t,DN=5-t
过N作NG⊥BC于点G
∵MN∥AB
易知△MNG为等腰直角三角形
∴MG=NG
易证△NCG∽△DCF
∴NG=![]() CN,CG=
CN,CG=![]() CN
CN
∴NG=![]() t,CG=
t,CG=![]() t
t
又∴MG=NG=![]() t
t
∵CM=MG+CG
∴10-2t=![]() t+
t+![]() t,解得t=
t,解得t=s(在0≤t≤5的范围内,所以是满足题意的)
(3)第一种情况,MC=MN过M作MH⊥CN于点H,
根据三线合一,H为CN中点CM=10-2t,CH=![]() CN=
CN=![]() t
t
易证△CMH∽CDF
∴CH=![]() CM,即
CM,即![]() t=
t=![]() (10-2t),解得t=
(10-2t),解得t=![]() s(在0≤t≤5的范围内,所以是满足题意的)
s(在0≤t≤5的范围内,所以是满足题意的)
第二种情况,MN=CN过N作NI⊥CM于点I,
根据三线合一,I为CM中点CN=t,CI=![]() CM=
CM=![]() (10-2t)
(10-2t)
易证△CNI∽△CDF
∴CI=![]() CN,即
CN,即![]() (10-2t)=
(10-2t)=![]() t,解得t=
t,解得t=![]() s(在0≤t≤5的范围内,所以是满足题意的)
s(在0≤t≤5的范围内,所以是满足题意的)
第三种情况,CM=CN,CM=10-2t,CN=t
∴10-2t=t,解得t=![]() s(在0≤t≤5的范围内,所以是满足题意的)
s(在0≤t≤5的范围内,所以是满足题意的)
综上,当t=![]() s,
s,![]() s,
s,![]() s时,△MNC为等腰三角形.
s时,△MNC为等腰三角形.
略








