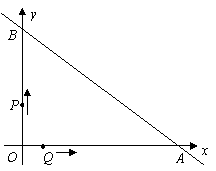
直线 与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
(1)直接写出A、B两点的坐标;
(2)设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式;
(3)当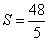 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
答案
(1)A(8,0),B(0,6)(2)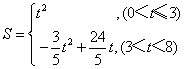 (3)M1(
(3)M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() )
)
知识点:运动变化型问题
第一步:研究基本图形.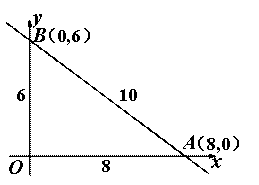
第二步:分析运动过程,研究动点的起点、终点和状态转折点,确定分类和时间范围.易判断P点速度为2cm/s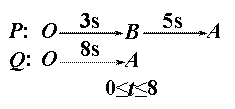
第三步:表达,根据几何特征建等式.
(1)分析基本图形的时候A、B两点坐标已求出,分别为(8,0),(0,6);
(2)①当0<t≤3时,点P在OB上运动,如图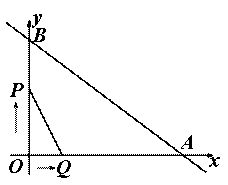
OP=2t,OQ=t∴S=![]() OP·OQ=
OP·OQ=![]() ·2t·t=t2
·2t·t=t2
②当3<t<8时,点P在BA上运动,如图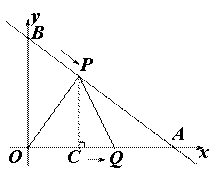
AP=6+10-2t=16-2t,OQ=t
易证△APC∽△ABO
∴PC=![]() AP=
AP=![]() (16-2t)
(16-2t)
∴S=![]() OQ·PC=
OQ·PC=![]() ·t·
·t·![]() (16-2t)=
(16-2t)=![]() t2+
t2+![]() t
t
综上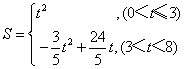
(3)根据(2)可以判断当![]() 时,点P在BA上运动,此时3<t<8,令
时,点P在BA上运动,此时3<t<8,令![]() t2+
t2+![]() t=
t=![]() ,解得t=4s由此可以计算点P的坐标为(
,解得t=4s由此可以计算点P的坐标为(![]() ,
,![]() ),Q点坐标为(4,0)
),Q点坐标为(4,0)
满足题意的M点有三个,M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() )
)
略








