如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
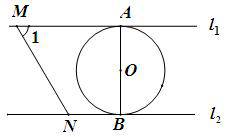
- A.
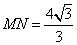
- B.若MN与⊙O相切,则
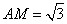
- C.若∠MON=90°,则MN与⊙O相切
- D.l1和l2的距离为2
答案
正确答案:B
解:利用平移的性质,
A.平移MN使点B与N重合,∠1=60°,AB=2,解直角三角形得MN=![]() ,正确;
,正确;
B.当MN与圆相切时,有两种情况,左边相切或右边相切,AM=![]() 或者
或者![]() ,错误;
,错误;
C.若∠MON=90°,连接NO并延长交MA于点C,则△AOC≌△BON,∴CO=NO,又∠MON=90°,∴∠MOC=90°,∴△MON≌△MOC(SAS),故MN上的高=MC上的高=OA=1,即O到MN的距离等于半径,故C正确;
D.l1∥l2,两平行线之间的距离为线段AB的长,直径AB=2,正确.
故选B.
略








