(上接第2,3题)(3)将矩形折叠,使点O与点F重合,折痕分别交x轴、y轴于点H,G,则线段OG的长为( )
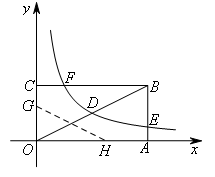
- A.
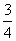
- B.
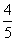
- C.
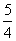
- D.
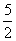
答案
正确答案:C
知识点:反比例函数与几何综合 翻折变换(折叠问题)
点击查看解析视频:http://v.xxt.cn/course/video.do?id=13090
1.解题要点
①OG是由折叠产生的,所以利用折叠来解决问题.
②利用折叠,借助勾股定理求出OG的长,操作过程中,注意找准目标,当假设的未知量是中间的某一个量时,注意最后还原成要求的目标.
③函数与几何综合的最后一问,是与几何知识融合的题目,在书写过程时,调用几何板块的书写模式.
2.解题过程
如图,连接GF.
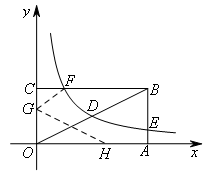
由折叠得,OG=GF.
∵BC∥OA,B(4,2),
∴点F的纵坐标为2.
∵![]() 的图象过点F,
的图象过点F,
∴F(1,2),
∴CF=1.
设OG=GF=x,则CG=2-x.
在Rt△CGF中,![]() ,
,
即![]() ,解得
,解得![]() ,
,
即OG的长为![]() .
.
略








