已知两个全等的直角三角形纸片ABC，DEF，如图放置，点B，D重合，点F在BC上，AB与EF交于点G，∠C=∠EFB=90°，∠E=∠ABC=30°，AB=DE=4．若纸片DEF不动，纸片ABC绕点F
逆时针旋转30°，则C到DE的距离为(    )

• A.4
• B.
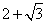
• C.
• D.

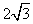
答案

正确答案：C

知识点：勾股定理  旋转的性质  

由第一个图可计算出，DF=2，
∴
在第二个图中，设BC与DE交于点P．
分析旋转三要素可知，∠DFP=30°．
∵∠D=60°，
∴∠CPD=90°，则CP的长即为所求．
在Rt△DPF中，∠DFP=30°，DF=2，
∴
∴
故选C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>