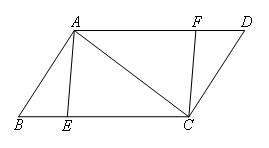
如图，在平行四边形ABCD中，AB=6，BC=10，对角线AC⊥AB，点E，F分别是边BC，AD上的点，且BE=DF．①当AE的长为( )时，四边形AECF是菱形；
②当AE的长为( )时，四边形AECF是矩形．
- A.5；
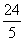
- B.6；
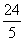
- C.5；
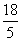
- D.6；
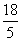
答案
正确答案：A
知识点：菱形的判定 矩形的判定 等面积法 平行四边形的性质和判定
在平行四边形ABCD中，
AD∥BC，AD=BC，
∵BE=DF，
∴AF=EC，
∴四边形AECF是平行四边形，
①当四边形AECF是菱形时，
AE=CE，
∵AC⊥AB，
∴∠BAC=90°，
又∵AE=CE，
∴AE=BE，
∴BE=CE，
即此时E为BC的中点，
AE=5，
②当四边形AECF是矩形时，
∠AEC=90°，
∵AB=6，BC=10，
∴AC=8，
由等面积法可知：
，
即
，
∴AE=4.8，
综上，选A
略
WORD格式（
