如图，把一张矩形纸片OABC放在平面直角坐标系xOy中，使OA，OC分别落在x轴、y轴的正半轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点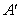
处．若
，
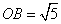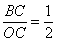，则点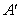的坐标为( )
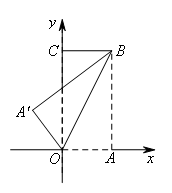
- A.
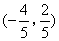
- B.
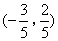
- C.
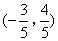
- D.
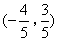
答案
正确答案：C
知识点：勾股定理 矩形的性质 轴对称的性质 翻折变换（折叠问题）
如图，过点
作
轴于点D，设
与OC交于点E．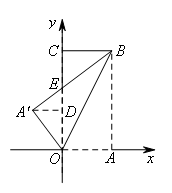
∵在Rt△OBC中，
，
，
∴OC=2，BC=1．
∵四边形OABC是矩形，
∴OA=BC=1，AB=OC= 2．
∵OC∥AB，
∴∠ABO=∠COB．
由折叠得，
，
∴
，EO=EB，
∴
．
设
，则
．
在
中，由勾股定理得，
，
解得
，
∴
．
∵
，
∴
，
∴点的坐标为
．
故选C．
略
WORD格式（
