在平面直角坐标系中，已知直线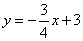与x轴、y轴分别交于点A，B，
点C（0，n）是y轴正半轴上一点．把坐标平面沿直线AC折叠，若点B恰好落在x轴上的点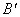处，则点C的坐标为(    )

• A.
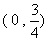
• B.
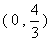
• C.
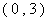
• D.

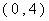
答案

正确答案：B

知识点：勾股定理  翻折变换(折叠问题)  一次函数综合题  

如图，连接．

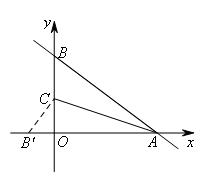
由题意得，A（4，0），B（0，3）．
在Rt△AOB中利用勾股定理得，AB=5．
由折叠性质可知，．
∵点C的坐标为（0，n），
∴OC=n，
∴．
在中利用勾股定理得，，
解得，，
∴点C的坐标为．
故选B．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>