如图,在半径为3的⊙O中,B是劣弧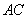 的中点,连接AB并延长至点D,使BD=AB,
的中点,连接AB并延长至点D,使BD=AB,
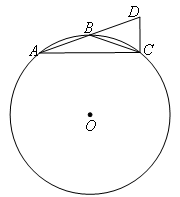
连接AC,BC,CD.若AB=2,则CD的长为( )
- A.2
- B.1
- C.
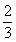
- D.
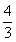
答案
正确答案:D
知识点:圆心角、弧、弦的关系 直角三角形斜边中线等于斜边一半
1.解题要点
由AB=BC=BD,可以得到△ACD是直角三角形;
圆背景下,B是劣弧![]() 的中点,连接圆心和点B,则OB垂直平分AC,
的中点,连接圆心和点B,则OB垂直平分AC,
之后借助勾股定理可以表达线段的长.
2.解题过程
由题意得,AB=BC.
∵BD=AB,
∴AB=BC=BD,
∴∠ACD=90°.
如图,连接OB,OA,设OB与AC相交于点E.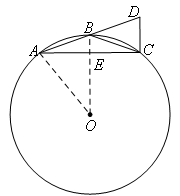
则OB⊥AC,AE=CE,
∴![]() .
.
设BE=a,则OE=3-a.
在Rt△AOE和Rt△ABE中,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
即![]() ,
,
∴![]() .
.
略








