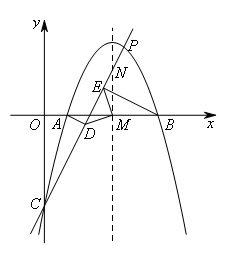
如图,抛物线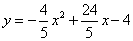 与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线的对称轴与x轴交于点M.P是x轴上方的抛物线上一动点(点P,M,C不在同一条直线上),过点A,B作直线CP的垂线,垂足分别为点D,E,连接MD,ME.
与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线的对称轴与x轴交于点M.P是x轴上方的抛物线上一动点(点P,M,C不在同一条直线上),过点A,B作直线CP的垂线,垂足分别为点D,E,连接MD,ME.
(1)若存在点P使得△MDE为等腰直角三角形,则点P的坐标为( )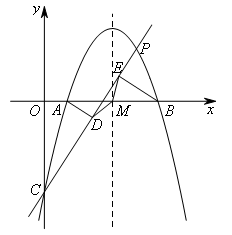
- A.(3,2)
- B.
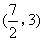
- C.(3,2)或(0,-4)
- D.
答案
正确答案:B
如图,延长DM交BE于点F.

∵AD⊥CP,BE⊥CP,
∴AD∥BE,
∴∠MBF=∠MAD.
又∵MA=MB,∠AMD=∠BMF,
∴△AMD≌△BMF,
∴MD=MF,即点M为Rt△EDF的斜边DF的中点,
∴MD=ME,即△MDE是等腰三角形.
要使得△MDE为等腰直角三角形,只需∠DME=90°即可.
如图,∠DME=90°,∠MDE=∠MED=45°,设直线CP与抛物线对称轴交于点N.
∵∠AMN=90°,
∴∠AMD=∠NME.
又∵MD=ME,∠ADM=∠NEM=135°,
∴△ADM≌△NEM,
∴MA=MN.
∵抛物线的解析式为![]() ,
,
∴抛物线的对称轴为直线x=3,A(1,0),B(5,0),C(0,-4),
∴M(3,0),MN=MA=2,
∴N(3,2).
由点C,N的坐标可求得直线CN的解析式为y=2x-4.
由![]() 得,
得,![]() ,
,
∴点P的坐标为![]() .
.
略








