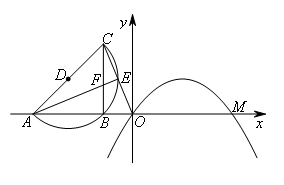
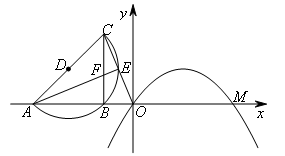
如图,在平面直角坐标系中,点A,B在x轴上,且点B的横坐标t满足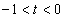 ,等腰三角形ABC的顶点B在以AC为直径的半圆D上,E是直线OC与半圆D的另一个交点,连接AE,交BC于点F.
,等腰三角形ABC的顶点B在以AC为直径的半圆D上,E是直线OC与半圆D的另一个交点,连接AE,交BC于点F.
(1)已知抛物线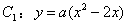 向左平移2个单位长度后,与x轴恰好交于A,O两点.若平移后所得抛物线
向左平移2个单位长度后,与x轴恰好交于A,O两点.若平移后所得抛物线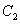 经过点F,则a可以用含t的代数式表示为( )
经过点F,则a可以用含t的代数式表示为( )
- A.
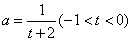
- B.
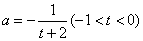
- C.
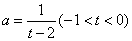
- D.
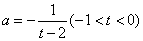
答案
正确答案:B
1.解题要点
①首先研究基本图形,再研究二次函数平移.
△ABC是等腰直角三角形,△CEF,△ABF,△CBO都是直角三角形.
根据抛物线![]() 的解析式可得
的解析式可得![]() ,由平移可得
,由平移可得![]() ,
,
∴![]() .
.
②抛物线![]() 经过点F,所以需要表达出点F的坐标,代入抛物线
经过点F,所以需要表达出点F的坐标,代入抛物线![]() 的解析式.
的解析式.
F是AE和BC的交点,观察图形可知△CEF∽△ABF∽△CBO.
∵AB=BC,
∴△ABF≌△CBO,
∴BF=BO=-t,
∴![]() ,代入抛物线
,代入抛物线![]() 的解析式可得a与t之间的关系式.
的解析式可得a与t之间的关系式.
2.解题过程
如图,
由题意得![]() ,
,
平移之后的抛物线为![]() .
.
∵AC是⊙D的直径,
∴∠ABC=∠CEA=90°.
∵∠AFB=∠CFE,
∴∠BAF=∠BCO.
又∵AB=BC,
∴△ABF≌△CBO(AAS),
∴BF=BO.
∵![]() ,
,
∴BO=BF=-t,
∴![]() .
.
∵![]() 经过点
经过点![]() ,
,
∴![]() ,
,
即a可以用含t的代数式表示为![]() .
.
略








