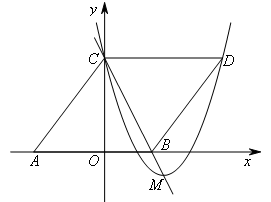
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-6,0),B(4,0),
C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线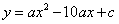 经过点C,顶点M
经过点C,顶点M
在直线BC上.若抛物线上一点P满足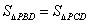 ,则点P的坐标为( )
,则点P的坐标为( )
- A.
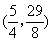
- B.
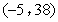
- C.
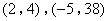
- D.
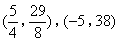
答案
正确答案:D
知识点:二次函数背景下的面积问题 面积处理思路 函数处理框架
1.解题要点
①首先研究基本图形,四边形ABDC是菱形,CD∥AB,容易求出点D的坐标.
抛物线的对称轴为直线![]() ,
,
进而可确定点M的坐标,求出抛物线的解析式.
②分析△PBD与△PCD,有公共边PD,调用“坐标系中的面积问题”,
利用转化法来分析问题,
当点B,C位于直线PD异侧时,PD过线段BC的中点;
当点B,C位于直线PD同侧时,PD∥BC.
③分类画图,对于每一种情形,借助图形基本信息,选取合适的方式求解.
2.解题过程
∵A(-6,0),B(4,0),C(0,8),
∴AB=AC=10,
∴四边形ABDC是菱形,
∴AB∥CD,CD=AB=10,
则点D的坐标为(10,8).
∵B(4,0),C(0,8),
∴![]() .
.
∵抛物线的对称轴为直线![]() ,
,
∴M(5,-2).
将点M(5,-2)和点C(0,8)代入抛物线解析式,
可得![]() .
.
①当点B,C位于直线PD异侧时,取BC的中点E,
作直线DE,交抛物线于另一点P,
则点P满足![]() ,如图所示,
,如图所示,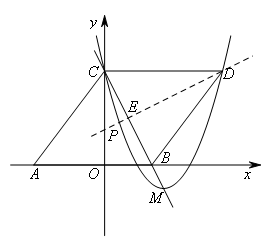
∵CD=BD,CE=BE,
∴DE⊥BC,
∴![]() .
.
联立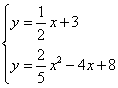 ,解得
,解得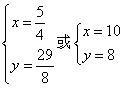 ,
,
∴![]() .
.
②当点B,C位于直线PD同侧时,过点D作DF∥BC,
交抛物线于另一点P,此时点P也满足![]() ,如图所示,
,如图所示,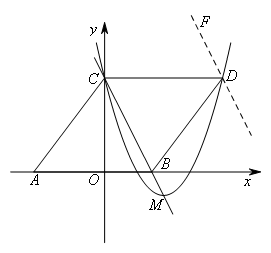
易得![]() ,
,
联立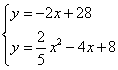 ,解得
,解得![]() ,
,
∴![]() .
.
综上,符合题意的点P的坐标为![]() .
.
略








