如图,已知点A,B分别在x轴和y轴上,且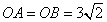 ,点C的坐标为
,点C的坐标为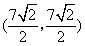 ,AB与OC相交于点G.点P从点O出发,以每秒1个单位长度的速度沿线段OC向点C运动,过点P作直线EF∥AB,分别交OA,OB或AC,BC于点E,F.设点P运动的时间为t秒(
,AB与OC相交于点G.点P从点O出发,以每秒1个单位长度的速度沿线段OC向点C运动,过点P作直线EF∥AB,分别交OA,OB或AC,BC于点E,F.设点P运动的时间为t秒(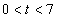 ).
).
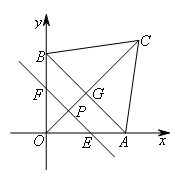
(1)若直线EF在四边形OACB内扫过的面积为S,则S与t之间的函数关系式为( )
- A.
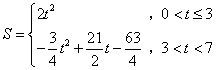
- B.

- C.
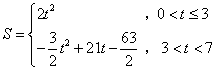
- D.
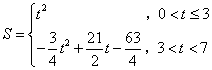
答案
正确答案:D
1.解题要点
①研究基本图形,研究边、角关系,发现OC垂直平分AB,OG=AG=3,CG=4,OC=7.
②分析运动状态,分段,定范围,以P在OG或CG上分别研究.
显然应该分为两段,即![]() .
.
③分段画图,设计方案表达面积.
2.解题过程
∵![]() ,
,
∴∠OAB=∠OBA=45°,AB=6.
∵![]() ,
,
∴OC是∠AOB的平分线,OC=7,
∴OC⊥AB,
∴OG=AG=BG=3.
∵EF∥AB,
∴EF⊥OC,OP=PE=PF(OC始终是线段EF和线段AB的垂直平分线).
当![]() 时,如图所示,
时,如图所示,
直线EF在四边形OACB内扫过的面积就是△OEF的面积.
∵OP=PE=PF=t,
∴![]() .
.
当![]() 时,如图所示,
时,如图所示,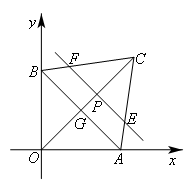
直线EF在四边形OACB内扫过的面积就是五边形OAEFB的面积.![]() .
.
∵EF∥AB,
∴△CFE∽△CBA,
∴![]() .
.
∵OP=t,CP=7-t,CG=4,
∴![]() ,
,![]() ,
,
∴![]() ,
,
则![]() .
.
综上,![]() S与t之间的函数关系式为
S与t之间的函数关系式为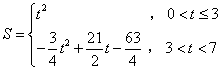 .
.
略







