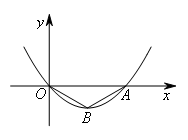
如图,已知抛物线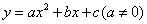 经过坐标原点O,交x轴于点A,顶点B的坐标为
经过坐标原点O,交x轴于点A,顶点B的坐标为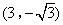 .Q是抛物线上的一动点(不与点B重合),当△AOQ与△AOB相似时,点Q的坐标为( )
.Q是抛物线上的一动点(不与点B重合),当△AOQ与△AOB相似时,点Q的坐标为( )
- A.
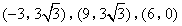
- B.
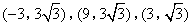
- C.
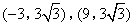
- D.
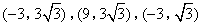
答案
正确答案:C
知识点:相似三角形的存在性
1.解题要点
①首先研究基本信息,求出抛物线解析式以及各点坐标.
②分析目标△AOB,是固定的三角形,OB=AB,∠OBA=120°;
△AOQ中,O,A是定点,Q是动点,
若两个三角形相似,△AOQ需要满足是等腰三角形,且顶角等于120°,
由图形关系可知,只能是∠OAQ=120°或∠AOQ=120°.
③分类分析,当∠OAQ=120°时,控制AQ=AO,满足△OAQ∽△OBA,
求出点Q的坐标,验证点Q是否在抛物线上;
当∠AOQ=120°时,类似分析.
2.解题过程
设![]() ,
,
∵点(0,0)在抛物线上,
∴![]() ,
,
∴![]() ,
,
∴A(6,0).
如图,过点B作BD⊥x轴于点D.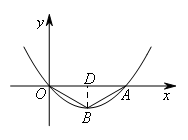
易知![]() ,
,![]() ,
,
∴∠AOB=∠OAB=30°,∠OBA=120°.
①如图,当∠OAQ=120°,且AQ=AO=6时,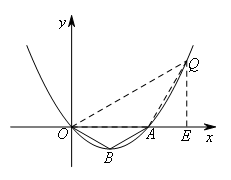
△OAQ∽△OBA,
过点Q作QE⊥x轴于点E,则AE=3,![]() ,
,
∴![]() ,
,
容易验证点![]() 在抛物线上,满足题意.
在抛物线上,满足题意.
②如图,当∠AOQ=120°,且QO=AO=6时,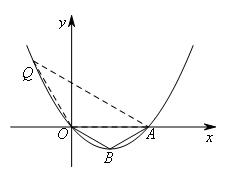
△QOA∽△OBA,
类比①可求点![]() 满足题意.
满足题意.
综上,符合题意的点Q的坐标为![]() .
.
略








