如图,分别以Rt△AOB的直角边OA,OB所在的直线为y轴、x轴建立平面直角坐标系,已知OA=2,OB=4,Q是边OB上的动点(不与点O,B重合),P是AB的中点.若以点O,P,Q为顶点的三角形与△AOB相似,则点Q的坐标为( )
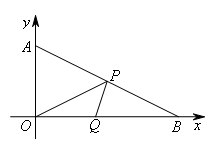
- A.
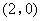
- B.

- C.

- D.
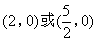
答案
正确答案:D
知识点:相似三角形的存在性
1.解题要点
①研究基本图形,对信息进行标注,![]() ,∠POQ=∠ABO.
,∠POQ=∠ABO.
②分析目标△AOB,是固定的直角三角形,两直角边之比为1:2;
△OPQ中,O,P为定点,∠POQ=∠ABO为不变特征,
若两个三角形相似,只需保证OQP=90°或∠OPQ=90°.
③分类画出符合题意的图形,根据比例关系建等式求解.
2.解题过程
在Rt△AOB中,OA=2,OB=4,
∴![]() .
.
∵P为AB中点,
∴![]() ,
,
∴∠POQ=∠ABO.
①当∠OQP=90°时,如图所示,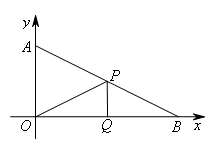
△OQP∽△BOA,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②当∠OPQ=90°时,如图所示,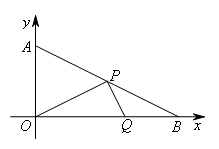
△OQP∽△BAO,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
综上,点Q的坐标为![]() .
.
略








