给出下列结论：
①一组对边平行，另一组对边相等的四边形是平行四边形；
②一组对边平行，一组对角相等的四边形是平行四边形；
③两组邻角互补的四边形是平行四边形；
④有一个角与相邻两角都互补的四边形是平行四边形．
其中正确的有(    )

处理概念类问题，一方面，需要和判定定理相匹配；另一方面，需要举反例．
①不是定理原话，可举出反例，如等腰梯形，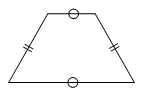

故结论①错误．
②不是定理原话，可考虑证明，
如图，已知四边形ABCD中，AD∥BC，∠B=∠D，
求证：四边形ABCD是平行四边形．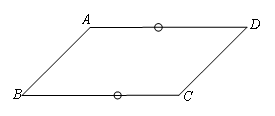

证明：∵AD∥BC，
∴∠A+∠B=180°．
∵∠B=∠D，
∴∠A+∠D=180°，
∴AB∥CD，
∴四边形ABCD是平行四边形．
故结论②正确（若令∠A=∠C也可证明）．
③不是定理原话，可举出反例，如梯形，
在如图所示的梯形中，∠1+∠2=180°，∠3+∠4=180°．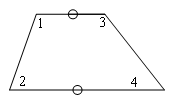

符合两组邻角互补，但不是平行四边形，
故结论③错误．
④不是定理原话，可考虑证明，
如图，已知四边形ABCD中，∠A+∠B=180°，∠A+∠D=180°.
求证：四边形ABCD是平行四边形．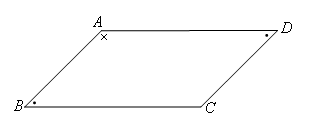

证明：∵∠A+∠B=180°，
∴AD∥BC，
同理，AB∥CD，
∴四边形ABCD是平行四边形，
故结论④正确．
综上，结论②，④正确，故选B．

略