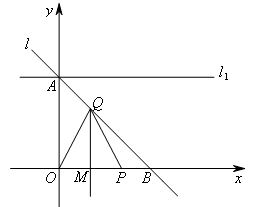
如图，已知直线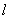经过A（0，1），B（1，0）两点，P是x轴正半轴上的一动点，且OP的垂直平分线交直线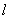于点Q，交x轴于点M，直线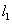经过点A且与x轴平行．若在直线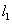上存在点C，使得
△CPQ是以Q为直角顶点的等腰直角三角形，则点C的坐标为(    )

1．解题要点
①观察题目特征，确定为等腰直角三角形存在性问题．
②分析定点、动点、不变特征．
③从已知出发，借助等腰直角三角形的性质（直角和两腰相等）和坐标系处理斜放置直角的原则，构造弦图模型解决问题．
2．解题过程
由题意得，OA=OB=1，△AOB为等腰直角三角形，点C的纵坐标为1．
①如图，当点Q在x轴上方时，延长MQ交直线于点E，则ME⊥．

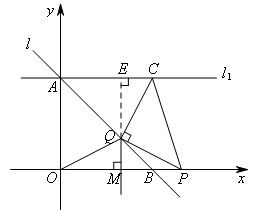
易证△CEQ≌△QMP，△QMB为等腰直角三角形，四边形AOME为矩形，
∴CE=QM=MB，AE=OM，
∴AC=AE+CE=OM+MB=OB=1，
∴点C的坐标为（1，1）．
②如图，当点Q在x轴下方时，延长QM交直线于点F．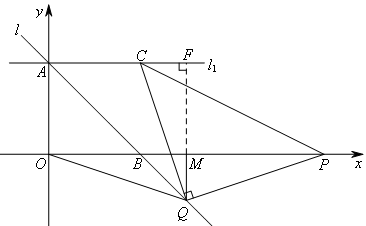

同理，得CF=QM=MB，AF=OM，
∴AC=AF-CF=OM-MB=OB=1，
∴点C的坐标为（1，1）．
综上得，点C的坐标为（1，1）．

略