如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为(    )

1．思路点拨：
见到垂直平分线要考虑垂直平分线的性质：垂直平分线上的点到线段两端点的距离相等，故想到连接AM，AN，出现等腰三角形．
2．解题过程：
如图，连接AM，AN．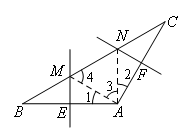

∵ME，NF分别为AB，AC的垂直平分线，
∴AM=BM，AN=CN，
∴∠1=∠B，∠2=∠C．
∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
即∠1=∠2=∠B=∠C=30°，
∴∠3=120°-30°-30°=60°，
∠4=2∠B=60°，
∴△AMN为等边三角形，
∴MN=AM=AN，
∴MN=BM=CN=2cm．
故选C．
3．易错点：
①不能结构化思考，对于见到垂直平分线要想到什么不清楚；
②能作出辅助线，但不知道借助等腰三角形进行边和角的互转．

略