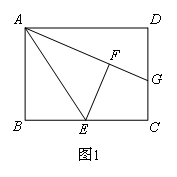
如图1,在长方形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,
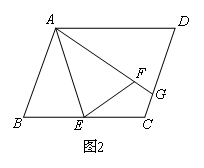
点F在矩形ABCD内部,延长AF交CD于点G,则FG=CG,请证明.小明发现把AE延长与GC的延长线交于一点H,证明△AHG是等腰三角形即可证明结论.如图2,将(1)中的长方形ABCD改为平行四边形,其他条件不变,我们可以结合小明的思路,延长AE与GC的延长线交于一点H,此时,证明△AHG是等腰三角形的依据是( )
- A.△AEG≌△HEG,全等三角形对应边相等
- B.AF=HC,FG=CG,等量加等量和相等
- C.∠CHE=∠FAE,等角对等边
- D.EG⊥AH,三线合一
答案
正确答案:C
知识点:类比探究问题
结合题意,延长AE与GC的延长线交于一点H.
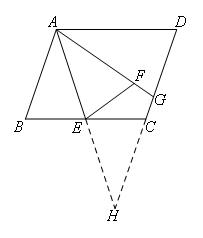
易证:△ABE≌△HCE,
∴∠BAE=∠CHE,AB=HC,
∵△ABE沿AE折叠后得到△AFE,
∴∠BAE=∠FAE,AB=AF,
∴∠CHE=∠FAE,
∴△AHG是等腰三角形,
∴AG=HG,
∴AG-AF=HG-HC,即:FG=CG.
证明△AHG是等腰三角形的依据是等角对等边,故选C
略









