如图1，在△ABC中，P为BC边的中点，直线a绕顶点A旋转，若B，P在直线a的异侧，
BM⊥直线a于点M，CN⊥直线a于点N，连接PM，PN．要证PM=PN，只需延长MP交CN于点E，通过说明某对三角形全等就可以证明此结论．此时，证明结论成立的理论基础是( )
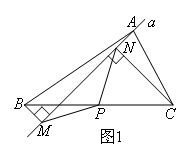
- A.全等三角形的对应边相等
- B.直角三角形斜边中线等于斜边一半
- C.等腰三角形等角对等边
- D.等量代换
答案
正确答案：B
知识点：类比探究问题
如图，延长MP交CN于点E.
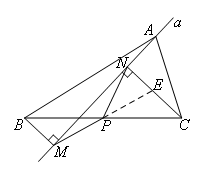
此时可证△MBP≌△ECP，
∴MP＝EP，
∵∠MNE＝90°，
∴PN＝PM＝PE，
即利用的是直角三角形斜边上中线等于斜边一半．
故选B
略
WORD格式（
