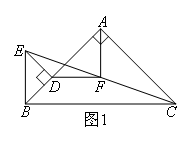
如图1,△ABC和△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,点D在AB边上.
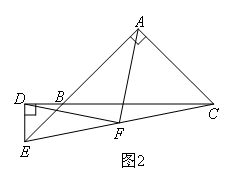
连接EC,取EC的中点F,连接AF,DF.为了证明FA⊥FD,FA=FD,我们只需要延长DF交线段AC于点G,说明AF是等腰直角三角形ADG的中线即可.将△BDE旋转至如图2所示的位置,使点E在AB的延长线上,点D在CB的延长线上,其他条件不变,类比上面的做法,为了证明FA⊥FD,FA=FD,我们需要作的辅助线是( )
- A.连接AD
- B.过点C作CG⊥DF,交DF的延长线于点G
- C.延长DF到G,使FG=DF,连接CG,AD,AG
- D.延长DF交AC的延长线于点G,连接AD
答案
正确答案:C
知识点:类比探究问题
在图1中,给出的辅助线达到的一个效果就是保证点F是等腰直角三角形ADG的斜边上的中点,满足FG=DF.
若在图2中达到同样的效果,需要延长DF到G,使FG=DF,
这样在连接AD,AG之后才能保证点F是等腰直角三角形斜边的中点.
故选C
略









