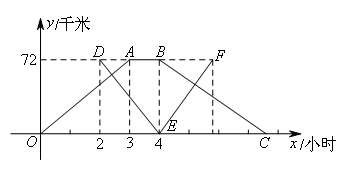
甲、乙两个港口相距72千米，一艘轮船从甲港出发，顺流航行3小时到达乙港，休息1小时后立即返回；一艘快艇在轮船出发2小时后从乙港出发，逆流航行2小时到达甲港，并立即返回（掉头时间忽略不计）．已知水流速度是2千米/时，下图表示轮船和快艇距甲港的距离y（千米）与轮船出发时间x（小时）之间的函数关系式（顺流速度=船在静水中速度+水流速度；逆流速度=船在静水中速度-水流速度）．请问快艇出发(    )小时，轮船和快艇在返回途中相距12千米？

由题意得，轮船从甲港出发，顺流航行3小时到达乙港，
∴轮船顺流航行的速度是72÷3=24千米/时，
∴轮船在静水中的速度是24-2=22千米/时，
轮船逆流航行的速度是22-2=20千米/时，
∴轮船逆流航行的时间为72÷20=3.6，
即C（7.6，0）．
设线段BC所在直线的解析式为y=kx+b，
∵B（4，72），C（7.6，0），
∴线段BC的解析式为．
∵快艇从乙港出发，逆流航行2小时到达甲港，
∴快艇逆流航行的速度为72÷2=36千米/时，
∴快艇在静水中的速度是36+2=38千米/时，
快艇顺流航行的速度是38+2=40千米/时，
∴快艇返回的时间是72÷40=1.8小时，
即F（5.8，72）．
设线段EF所在直线的解析式为y=mx+n，
∵E（4，0），F（5.8，72），
∴线段EF的解析式为．
轮船和快艇在返回途中相距12千米，
则40x-160-（-20x+152）=12或-20x+152-（40x-160）=12，
解得x=5.4或x=5，均符合题意，
∴快艇出发3小时或3.4小时，轮船和快艇在返回途中相距12千米．
故选D．

略