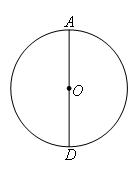
如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别是：
甲：1．作OD的中垂线，交⊙O于B，C两点；2．连接AB，AC，△ABC即为所求的三角形．
乙：1．以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点；2．连接AB，BC，CA,△ABC即为所求的三角形．
对于甲、乙两人的作法，可判断(    )

先按照甲、乙的作法，画出符合题意的图形，再去分析边和角，判定是否为等边三角形．
甲：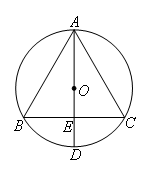
如图所示（E是半径OD的中点，BC经过点E且垂直AD）
由题意得BE=EC，弧BD=弧CD，
∴AD是BC的垂直平分线，
∴AB=AC．
连接OB，如图所示，

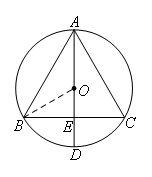
在Rt△OBE中，，
∴∠OBE=30°，∠BOE=60°，
∴，
∴，
∴∠BAC=60°，
∴△ABC是等边三角形，
即甲的作法正确．
乙：如图所示（残缺的圆弧在以点D为圆心，OD长为半径的圆上），
连接OB，BD，OC，CD．

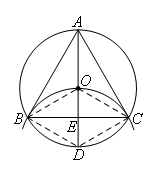
由题意得，△OBD和△OCD是等边三角形，四边形OBDC是菱形，
∴∠BOD=∠COD=60°，OD垂直平分BC，
∴AB=AC，，，
∴，
∴△ABC是等边三角形，
即乙的作法正确．

略