长为20,宽为a的长方形纸片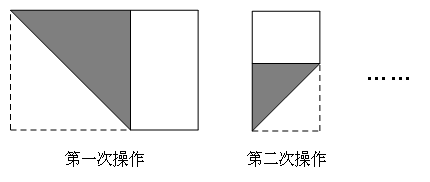
- A.10
- B.12
- C.12或15
- D.12或10
答案
正确答案:C
知识点:折叠问题
由题意,可知当10<a<20时,第一次操作后剩下的长方形的长为a,宽为20-a,
但是不清楚此时两边的大小,即此时a的大小影响长方形的长和宽,故需分类讨论:
①如果20-a>2a-20,即![]() ,那么第三次操作时正方形的边长为2a-20.
,那么第三次操作时正方形的边长为2a-20.
则2a-20=(20-a)-(2a-20),解得a=12;
②如果20-a<2a-20,即![]() ,那么第三次操作时正方形的边长为20-a.
,那么第三次操作时正方形的边长为20-a.
则20-a=(2a-20)-(20-a),解得a=15.
∴当n=3时,a的值为12或15.故选C
略








