在△ABC中,AB=AC,∠BAC=36°,作出AB边的垂直平分线DE,交AC于点D,交AB于点E,
连接BD,下列四个结论①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D点是AC的中点,正确的是(    )

如图．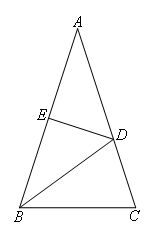

∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°．
∵DE垂直平分AB，
∴DA=DB，
∴∠ABD=∠A=36°．
∴∠DBC=36°，∠BDC=72°，
∴BD平分∠ABC；故①正确
AD=BD=BC；故②正确
△BCD的周长=BC+BD+CD
=BC+AD+CD=BC+AC=BC+AB；故③正确
∵BD＞CD，
∴AD＞CD．故④错误．
故答案为①②③．
故选A

略