如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
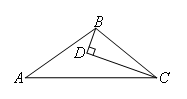
- A.1
- B.1.5
- C.2
- D.2.5
答案
正确答案:A
知识点:由三线合一想到补全等腰三角形
如图,延长BD,交AC于点E.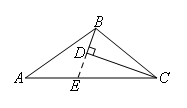
∵CD平分∠ACB,BD⊥CD,
∴△BEC是等腰三角形,即BC=CE.
∴BD=DE,
∵∠A=∠ABD,
∴AE=BE,
∵AC=5,BC=3,
∴AE=AC-CE=AC-BC=2,
∴![]()
故选A.
略




正确答案:A
知识点:由三线合一想到补全等腰三角形
如图,延长BD,交AC于点E.
∵CD平分∠ACB,BD⊥CD,
∴△BEC是等腰三角形,即BC=CE.
∴BD=DE,
∵∠A=∠ABD,
∴AE=BE,
∵AC=5,BC=3,
∴AE=AC-CE=AC-BC=2,
∴![]()
故选A.
略
