如图,在平行四边形ABCD中,AB:AD=3:2,∠ADB=60°,则cosA的值为( )
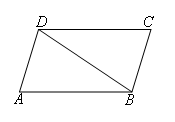
- A.
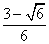
- B.
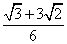
- C.
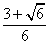
- D.
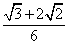
答案
正确答案:A
要求cosA的值,我们需要把∠A放到直角三角形当中,考虑∠ADB=60°,我们过点B作AD的垂线,从而把∠A和∠ADB都放到直角三角形中,这个时候只要求AE与AB的关系即可.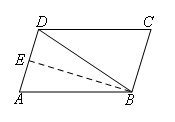
如图,过点B作BE⊥AD于点E,
∵AB:AD=3:2,
我们不妨设AB=3a,AD=2a.
在Rt△DEB中,
∵∠ADB=60°,
∴![]() ,
,
设DE=b,则![]() ,AE=2a-b.
,AE=2a-b.
在Rt△AEB中,AB=3a,![]() ,AE=2a-b,
,AE=2a-b,
由勾股定理可得![]() ,
,
解得![]() .
.
∴![]() ,
,
则在Rt△AEB中,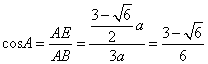 .
.
略








