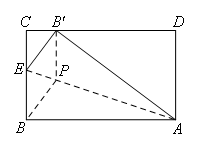
如图,在长方形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为
AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为( )
- A.1
- B.
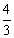
- C.
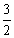
- D.
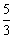
答案
正确答案:D
1.思路分析
本题主要考查折叠背景下灵活使用勾股定理建等式.解决此类问题需要:
①读题标注,梳理信息,明确目标.本题求解相等距离是多少,通过分析可知求解的是
B′P的长.
②清楚折叠性质,合理转化条件.折叠前后对应边、对应角相等,故B′P=BP,结合已知
点P到CD的距离与到点B的距离相等,可知B′P⊥CD.因此∠B′PE=∠BEP,进而可知
BE=BP=B′P=B′E.
③勾股定理建等式求解.在△B′CE中借助勾股定理建等式,求解B′P.
2.解题过程
由折叠可知,AB=AB′,B′P=BP,B′E=BE,∠B′PE=∠BPE
∵点P到CD的距离与到点B的距离相等
∴B′P即为点P到CD的距离,B′P⊥CD
∴B′P//BC
∴∠B′PE=∠BEP=∠BPE
∴BP=BE
∴BE=BP=B′P=B′E
在Rt△AB′D中,AB′=5,AD=3
由勾股定理得,B′D=4
∴B′C=5-4=1
在Rt△B′CE中,B′E=x,CE=3-x
由勾股定理得,B′E2=B′C2+CE2
∴![]()
故选D
3.易错点
不能将“点P到CD的距离与到点B的距离相等”合理转化,得出垂直的结论.
没有意识到通过平行转移角,进而转移相等的边,建等式求解.
略








