如图,在边长为6的正方形ABCD的内部有一点P,BP=4,∠PBC=60°.若点Q为正方形ABCD边上一点,且△PBQ是等腰三角形,则符合条件的点Q有( )个.
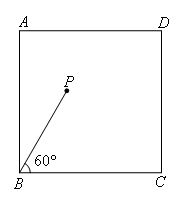
- A.3
- B.5
- C.6
- D.7
答案
正确答案:B
由于存在性问题所导致的分类讨论.
①当PB=PQ时,以点P为圆心,PB的长为半径作圆,
此时⊙P与CD边相切.
相切的理由:如图,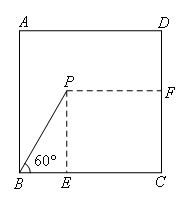
过点P作PE⊥BC,垂足为点E,作PF⊥CD,垂足为点F,容易求得BE=2,PF=4=PB.
∴此时⊙P与正方形ABCD的边交于![]() 三点,如图所示:
三点,如图所示: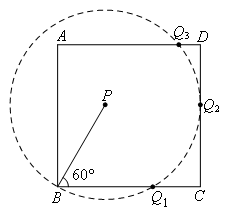
②当BQ=BP时,以点B为圆心,BP的长为半径作圆.
此时⊙B与正方形ABCD的边交于![]() 两点,如图所示:
两点,如图所示:
容易证明![]() 重合.
重合.
③当BQ=PQ时,作线段BP的垂直平分线,与正方形ABCD的边交于![]() 两点,如图所示:
两点,如图所示: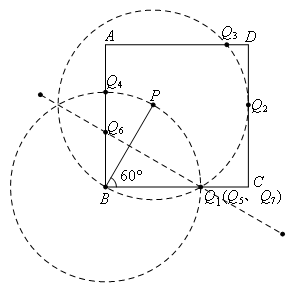
容易证明![]() 重合.
重合.
综上所述,符合条件的点Q有5个.
略








