已知一次函数y=kx+b的图象可以看作是由直线y=2x向上平移6个单位长度得到的,
且y=kx+b与两坐标轴围成的三角形面积被一正比例函数分成面积的比为1:2的两部分,
则这个正比例函数的解析式为( )
- A.
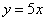 或
或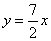
- B.
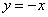 或
或
- C.
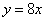 或
或
- D.
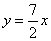 或
或
答案
正确答案:B
知识点:一次函数围成的三角形面积
∵y=kx+b的图象是由y=2x向上平移6个单位长度得来的
∴一次函数的解析式为:y=2x+6
如图所示,

y=2x+6与两坐标轴的交点坐标为A(-3,0),B(0,6),
其与两坐标轴围成的三角形的面积为![]()
∵一正比例函数将它分成面积为1:2的两部分
∴分成的两三角形面积分别为6,3
设所求正比例函数与一次函数y=2x+6交于点C(m,n)
分如下两种情况:
①当S△AOC=3时
∵OA=3,∴n=2
∴C(-2,2)
此时正比例函数的解析式为y=-x
②当S△AOC=6时
∵OA=3,∴n=4
∴C(-1,4)
此时正比例函数的解析式y=-4x
综上可知,正比例函数的解析式为y=-x或y=-4x.
故选B.
略







