如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,交半圆O于点D,则AD的长为( )

- A.
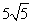 cm
cm - B.
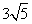 cm
cm - C.4cm
- D.
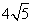 cm
cm
答案
正确答案:D
知识点:垂径定理 圆周角定理 相似三角形的性质和判定
方法一:如图,连接OD,OC,作DE⊥AB于E,OF⊥AC于F,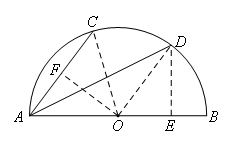
∵∠CAD=∠BAD,
∴弧CD=弧BD,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△OED,
∴OE=AF=![]() AC=3cm,
AC=3cm,
在Rt△DOE中,DE=4cm,
在Rt△ADE中,AD=![]() cm.
cm.
方法二:由直径想到圆周角,进而连接BC,BD,OD,设线段CB与AD交于点E,与OD交于点F,则如下图所示: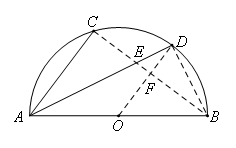
容易证明,在Rt△ABC中,BC=8cm.OD∥AC,
∴点F是BC的中点,OF是△BCA的中位线
∴OF=3cm,BF=CF=![]() cm
cm
∵△DFE∽ACE,且DF=2cm,AC=6cm,
∴![]() ,
,
则EF=1cm,CE=3cm,
∴CE:AC=1:2
∵△CAE∽△DAB,
∴DB:AD=1:2
在Rt△DAB中,由勾股定理可以得到AD=![]() cm.
cm.
方法三:还记得可以用相似来证明的“三角形内角平分线分对边所成的两条线段,和两条邻边成比例”,这个定理吗?这个题目也可以借助于这个来做(有兴趣的同学可以尝试一下,连接BC,连接BD)
略








