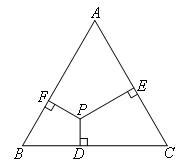
如图,等边△ABC内有一点P到三边的距离分别为h1,h2,h3,其中PD=h1,PE=h2,PF=h3,且
h1+h2+h3=6,则△ABC的面积为( )
- A.
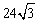
- B.
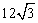
- C.
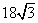
- D.
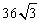
答案
正确答案:B
如图,连接AP,BP,CP,过点A作AG⊥BC于点G.

设等边△ABC边长为a,
则BG=GC=![]()
∴AG![]()
∴![]()
由题意知S△ABC=S△BCP+S△ACP+S△ABP=![]() a(h1+h2+h3),
a(h1+h2+h3),
∴![]() a(h1+h2+h3)
a(h1+h2+h3)![]() ,
,
∵h1+h2+h3=6,
∴a=![]() ,
,
∴![]() .
.
略








