如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,2),将矩形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E.那么点D的坐标为( )

- A.
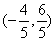
- B.
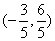
- C.
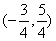
- D.
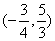
答案
正确答案:B
如图,过D作DF⊥x轴于F,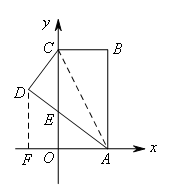 ∵点B的坐标为(1,2),∴AO=1,AB=2,根据折叠可知:CD=OA=1,而∠CDA=∠AOE=90°,∠DEC=∠AEO,∴△CDE≌△AOE,∴OE=DE,设OE=x,则CE=2-x,DE=x,∴在Rt△DCE中,CE2=DE2+CD2,∴(2-x)2=x2+12,∴
∵点B的坐标为(1,2),∴AO=1,AB=2,根据折叠可知:CD=OA=1,而∠CDA=∠AOE=90°,∠DEC=∠AEO,∴△CDE≌△AOE,∴OE=DE,设OE=x,则CE=2-x,DE=x,∴在Rt△DCE中,CE2=DE2+CD2,∴(2-x)2=x2+12,∴![]() ,又DF⊥AF,∴DF∥EO,∴△AEO∽△ADF,∴
,又DF⊥AF,∴DF∥EO,∴△AEO∽△ADF,∴![]() =
=![]() =
=![]() ,而AD=AB=2,∴AE=CE=2-
,而AD=AB=2,∴AE=CE=2-![]() =
=![]() ,即
,即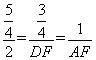 ,∴DF=
,∴DF=![]() ,AF=
,AF=![]() ,∴OF=
,∴OF=![]() -1=
-1=![]() ,∴D的坐标为(-
,∴D的坐标为(-![]() ,
,![]() ).故选:B.
).故选:B.
略








