已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点．连接AC，BD交于点P．
（1）如图1，当D为OA中点时，求的值；
（2）如图2，当AD:DO=1:m时，求的值；
（3）如图3，把题目中“点C为OB中点”改为“BC:CO=1:n”，当AD:DO=1:m时，直接写出的值．

答案

解：（1）如图1，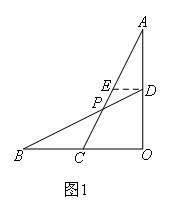

过点D作DE∥OB交AC于点E，∠ADE=∠O，∠AED=∠ACO
∴△ADE∽△AOC
∴
又∵DE∥OB
∴∠EDP=∠B，∠DEP=∠BCP
∴△DEP∽△BCP
∴
∴=2
（2）如图2，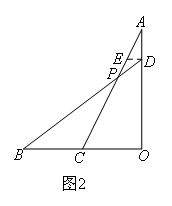

过点D作DE∥OB交AC于点E，∠ADE=∠O，∠AED=∠ACO
∴△ADE∽△AOC
∴，
∵DE∥OB
∴∠EDP=∠B，∠DEP=∠BCP
∴△DEP∽△BCP
∴
∴
设AE=k，则EC=mk
∴EP=
∴AP=AE+EP=，PC=EC－EP=
∴=
（3）

知识点：相似中的类比探究问题  

略

略

下载次数：2

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>