（1）如图1，已知正方形ABCD，E是AD上一点，F是BC上一点，G是AB上一点，H是CD上一点，线段EF，GH交于点O，∠EOH=∠C．求证：EF=GH；
（2）如图2，若将“正方形ABCD”改为“矩形ABCD”，且AD=mAB，其他条件不变，探索线段EF与线段GH的数量关系并加以证明；
（3）根据前面的探究，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题，画出图形，并证明；若不能，说明理由．
答案
证明：（1）如图1，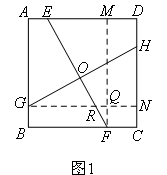
过点F作FM⊥AD于M，过点G作GN⊥CD于N则FM=GN=CD=BC，且GN⊥FM，设它们的垂足为Q，EF，GN交于点R
∵∠EOH=∠GOF=∠C=90°，
∴ ∠OGR=90°-∠GRO=90°-∠QRF=∠OFM．
∵ ∠GNH=∠FME=90°，FM=GN，
∴ △GNH≌△FME．
∴EF=GH
（2）GH=mEF
证明如下：如图2，
过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF，GN交于点R，GN，MF交于点Q
∵∠EOH=∠GOF=∠C=90°，
∴ ∠OGR=90°-∠GRO=90°-∠QRF=∠OFM．
∵ ∠GNH=∠FME=90°，
∴ △GNH∽△FME．
∴
=m，即：GH=mEF
（3）如图，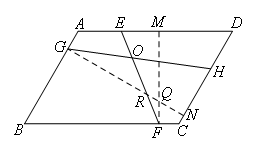
已知平行四边形ABCD，E是AD上一点，F是BC上一点，G是AB上一点，H是CD上一点，线段EF，GH交于点O，∠EOH=∠C，AD=mAB，则GH=mEF．
证明：如图，过点F作FM⊥AD于M，过点G作GN⊥CD于N，设EF，GN交于点R、GN，MF交于点Q，
在四边形MQND中，∠QMD=∠QND=90°
∴ ∠ADC+∠MQN=180°．
∴ ∠MQN=∠C=∠EOH=∠GOF．
∵ ∠ORG=∠QRF，
∴ ∠HGN=∠EFM．
∵ ∠FME=∠GNH=90°，
∴ △GNH∽△FME．
∴
∵AB
GN=ADMF
∴
=m
∴
，即：GH=mEF
知识点：相似中的类比探究问题
略
略
WORD格式（
