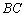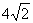（2009山西太原）如图，在等腰梯形ABCD中，AD//BC，=4AD=，∠B=45°．直角三角板含45°角的顶点E在边BC上移动，一直角边始终经过点A，斜边与CD交于点F．若△ABE为等腰三角形，则CF的长等于_______________．

解：根据已知条件可得，
AB=（BC-AD）÷2÷cosB=3，
①AB=AE（AE′）时，如图，


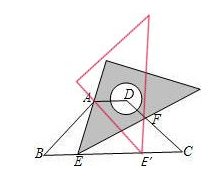
∠B=45°，∠AE′B=45°，
∴AE′=AB=3，
则在Rt△ABE′中，BE′=，
故E′C=．
易得△FE′C为等腰直角三角形，
故FC =2．
②当AB=BE″时，

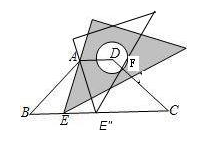
易得△E″CF为等腰三角形，
∴CF=CE″=-3；
②AE=BE时，


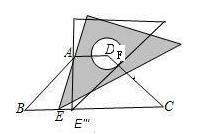
△ABE′″和△CFE′″是等腰Rt△，
∴BE′″=，
∴CE′″=
∴CF=FE′″=．
故答案为：2，-3，

学生不能够分三种情况讨论或则情况讨论不全。