关于x的方程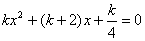有两个不相等的实数根.（1）求k的取值范围；（2）是否存在实数k，使方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由.

答案

解：（1）∵x的方程有两个不相等的实数根．
∴，
∴k+1＞0，∴k＞- 1，且k≠0；
（2）∵当方程两个实数根的倒数和等于0，
∴，
∴，
∴，
∵，
∴k=-2，
∵k＞- 1，且k≠0；
∴不存在实数k，使方程两个实数根的倒数和等于0．

知识点：根的判别式  

（1）根据x的方程有两个不相等的实数根，得出，即可得出答案；（2）当方程两个实数根的倒数和等于0，得出，进而得出k的值从而得出答案．

在解不等式时一定要注意数值的正负与不等号的变化关系，以及注意二次项系数不能为0，求出k的值必须在第一问中k的取值范围中。

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>