如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN（不必写出证明过程）（1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=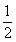
∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=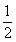∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．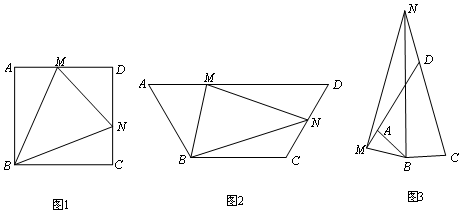
∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=
答案
解：（1） 图2，猜想：MN=AM+CN如图，延长NC至点F，使CF= AM，连接BF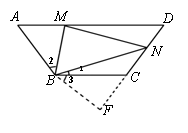
∵四边形ABCD是等腰梯形
∴∠DAB=∠ADC又
∵AD∥CB
∴∠ADC =∠BCF
∴∠BCF=∠DAB又∵AB=BCAM=CF
∴△AMB≌△CFB
∴∠2=∠3BM=BF
∵∠MBN=
∠ABC
∴∠1+∠2=∠MBN
∴∠1+∠3=∠MBN即∠MBN=∠NBF
又∵BN=BNBM=BF
∴△MBN≌△FBN
∴MN=NF
∵NF=NC+CF
∴MN=AM+CN
（2）图3猜想：MN=CN-AM
略
略
WORD格式（
