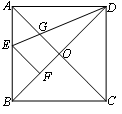
如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合.展开后，折痕DE分别交AB、AC于点E、G.连接GF.下列结论：①∠AGD=112.5°；②AD=2AE；③S_△AGD=S_△OGD；④四边形AEFG是菱形；⑤BE=2OG.
其中正确结论的序号是（ ）

解：①∵DE为折痕
∴∠ADE=∠BDE=∠ADB=22.5°
∵在△AGD中，∠DAC=45°
∴∠AGD=180°-22.5°-45°=112.5°，①正确
②设AE=x，则有折叠后两图形全等知：EF=AE=x
∵Rt△BEF为等腰直角三角形
∴BE=EF=x
∴AD=AB=AE+EB=（+1）x≠2AE，②错误
③过点G作GH⊥AD交AD于H

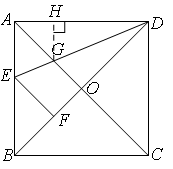
则有角平分线性质：GH=OG
从而S_△HGD=S_△OGD
显然S_△HGD≠S_△AGD
③错误
④连接GF

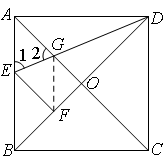
∵∠AGD=112.5°
∴∠2=67.5°
∵∠1=67.5°
∴AE=AG
由折叠知：AE=EF
从而AE=EF=FG=GA
∴四边形AEFG是菱形（四条边相等的四边形为菱形）
④正确
⑤有②中结论知：EB=AE
又知道OG=GH=AG
∵AE=AG
∴BE=2OG
⑤正确

条件太多，理不出头绪