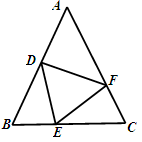
已知：如图，在△ABC中，AB=AC，D、E、F分别为AB、BC、CA上的点，且BD=CE，∠DEF=∠B．证明：△DEF是等腰三角形

答案

证明：∵AB=AC，∴∠B=∠C
∵∠CED=∠B+∠EDB，又∠DEF=∠B
∴∠FEC=∠EDB
在△DBE和△EFC中
∠EDB=∠FEC
DB =EC
∠B =∠C
∴△DBE≌△ECF
∴ED=EF
∴△DEF为等腰三角形

知识点：等腰三角形的判定与性质  

根据角度关系寻找全等的条件

角度的转移

下载次数：5

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>