如图，在等腰梯形ABCD中，AD∥BC，BC=4AD=4，∠B=45°，直角三角板含45°角的顶点E在边 BC上移动，一直角边始终经过点A，斜边与CD交于点F，若△ABE为等腰三角形，则CF的长为______.

A. $\frac{5}{4}\sqrt{2}$
B. $\sqrt{2}$
C. $\frac{5}{4}\sqrt{2}$ 或 $\sqrt{2}$
D. $\frac{5}{4}\sqrt{2}$ ， $\sqrt{2}$ 或 $4-\frac{3}{2}\sqrt{2}$

答案

正确答案：D

①当AE=BE时，因为∠B＝∠AEF＝45°，△EAM，△DFM是等腰直角三角形。又根据等腰梯形的性质，可以知道，AB=DC= $\frac{3}{2}\sqrt{2}$ ，AM=AE= $\frac{3}{2}$ ，DF= $\frac{\sqrt{2}}{4}$ ，CF=CD-DF= $\frac{5\sqrt{2}}{4}$

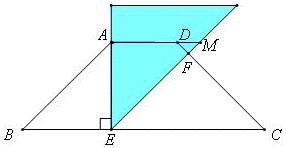
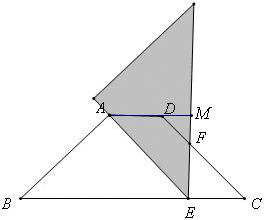
②当AB=AE时，如图，AM=ME= $\frac{3}{2}$ ，DM=AM-AD= $\frac{1}{2}$ ，DF= $\frac{\sqrt{2}}{2}$ ，CF=CD-DF= $\sqrt{2}$

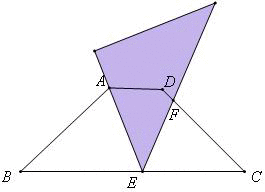
③当AB=BE时，如图，∠BAE=∠BEA=67.5°，则计算可得∠CEF=∠EFC=67.5°，CF=CE=BC-BE=4- $\frac{3}{2}\sqrt{2}$ ，故答案为D

对题中存在的各种情况考虑不全，不能将答案填完整

下载次数：0

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>