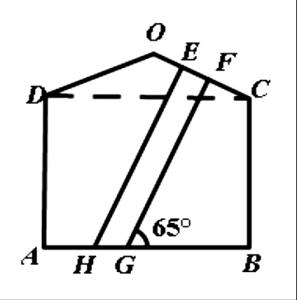
(2011江苏)一幢房屋的侧面外壁的形状如图所示,它由等腰△OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°. (参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m)
答案
证明:(1)∵矩形ABCD中,DC∥AB,∠FGB=65°.
∴∠FMC=∠FGB=65°,
∵∠OCD=25°,
∴∠MFC=90°,
∴GF⊥CO;
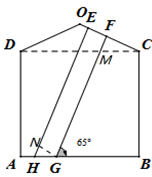
解:(2)做CN⊥EH,交EH于点N,
∵GF⊥CO;FG∥EH,
∴OC⊥EH,
∴四边形ENGF是矩形;
∴EF=NG,
∵∠FGB=∠NHG=65°,
∴sin65°= = 2.6NG≈0.91,
∴NG=2.366≈2.4.
知识点:平行线的性质 等腰三角形的性质 直角三角形的性质 矩形的性质
(1)根据∠OCD=25°,矩形ABCD,∠FGB=65°,得出∠FMC=65°,即可得出答案.
(2)根据矩形的判定得出EF=NG,再利用解直角三角形的知识得出NG的长.
找不到EF=HG这一对等量关系。对图形认识不清。








