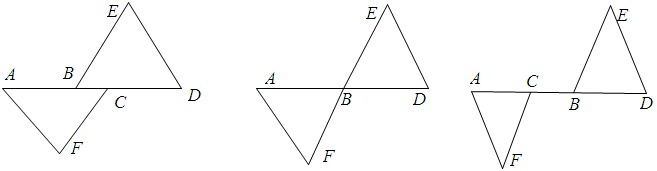
如图,A、B、C、D在同一直线上,AB=CD,DE∥AF,且DE=AF,求证:△AFC≌△DEB.如果将BD沿着AD边的方向平行移动,如图,B点与C点重合时,如图,B点在C点右侧时,其余条件不变,结论是否仍成立,如果成立,请予证明;如果不成立,请说明理由.
答案
①证明:∵DE∥AF,∴∠A=∠D
∵AB=CD,∴AB+BC=CD+BC即AC=BD
在△AFC和△DEB中
∴△AFC≌DEB(SAS)
②成立。
∵DE∥AF,∴∠A=∠D
在△AFC和△DEB中
∴△AFC≌DEB(SAS)
③成立
∵DE∥AF,∴∠A=∠D
∵AB=DC
∴AB-BC=DC-BC即AC=DB
在△AFC和△DEB中
∴△AFC≌DEB(SAS)
知识点:全等三角形的判定
分析运动过程中的不变关系,从而找出等量关系证明全等。
变化过程的分析,等量关系的确定。








