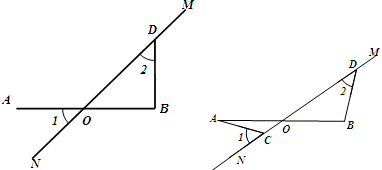在图中,直线MN与线段AB相交于点O,∠1 = ∠2 = 45°.
(1) 如图,若AO = OB,请写出AO与BD 的数量关系和位置关系;
(2) 将图中的MN绕点O顺时针旋转得到下图,其中AO = OB.
求证:AC = BD,AC ⊥ BD;
答案
解:(1)AO=DB且AO⊥DB
证明:∠DOB=∠1=45°=∠2
∴∠OBD=90°,OB=DB
又AO=OB,OB⊥BD,A、O 、B在同一直线上
∴AO=DB ,AO⊥DB。
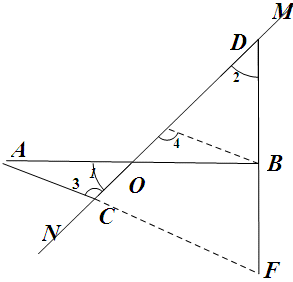
(2)证明:如图过B作BE∥AC交MN于点E,延长AC交DB的延长线于点F。
∠A=∠EBO,∠3=∠4
在△AOC和△BOE中
∴△AOC≌△BOE(AAS)
∴AC=BE
∵∠3=∠4=180°-∠1=135°,∴∠DEB=45°=∠2
在△EBD中,∠EBD=180°-45°-45°=90°
∴EB⊥BD,EB=BD
∴AC=BD
由于BE∥AF,∠EBD=90°
∴∠F=90°
∴AC⊥BD
知识点:全等三角形的判定与性质
构造全等三角形得出线段的等量关系和位置关系。
全等辅助线的做法